1 qp 312 60 48 50 502 56 510 1 qp 312 60 502 50 510. Aip Saripudin Bab 3 Matriks Sistem Persamaan Linear dan Determinan - 39 CONTOH 1 Tentukan solusi sistem persamaan linear berikut.

Penggunaan Matriks Untuk Menyelesaikan Sistem Persamaan Linear Matematika Sbmptn Un Sma Youtube
6 5 3 7 2 2 x y x y z x z Penyelesaian Matriks yang diperluas yang sesuai dengan sistem persamaan di atas adalah 4 7 2 2 1 0 6 5 3 2 0 1.
Persamaan linear meggunakan kaedah matriks. 6x 3y 24 5x 2y 18 Seterusnya menggunakan kaedah matriks hitung nilai x dan nilai y. Contoh ini menunjukkan bagaimana untuk memecahkan sistem persamaan linear di Excel. Jika A merepresentasikan matriks.
Sehingga diperoleh dua buah persamaan seperti berikut. Menggunakan kaedah matriks Add to my workbooks 7 Download file pdf Add to Google Classroom Add to Microsoft Teams Share. Dalam bidang aljabar linear Aturan Cramer Cramers Rule merupakan formula yang dipakai untuk menyelesaikan sistem persamaan linear dengan menggunakan determinan dari matriks yang terbentuk dari koefisien dan konstanta masing-masing persamaan di sistem tersebut.
Peringkat Matrix bergantung kepada baris dan lajur matriks. B Tulis persamaan linear serentak berikut dalam bentuk matriks. Matriks ini mempunyai 1 baris dan 4 lajur.
143 Menyelesaikan persamaan linear serentak dengan kaedah matriks. Satu matriks yang mempunyai m baris dan n lajur dikenal sebagai matriks peringkat m x n. Bentuk persamaan yang menyatakan hubungan antara x dan y dari persamaan 6 xy 0.
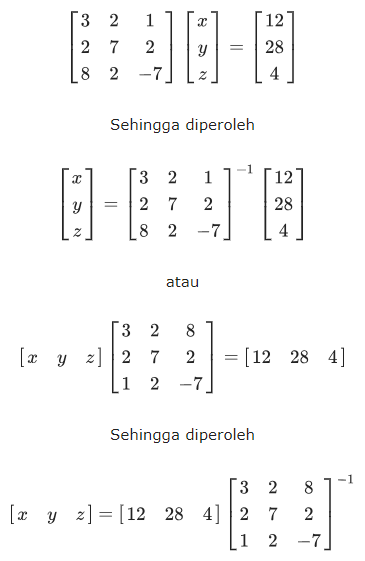
Tentukan nilai x dan y yang memenuhi sistem persamaan linear. Setelah ditulis ke dalam persamaan matriks sistem tersebut dapat diselesaikan dengan menggunakan matriks invers dan langkah-langkah berikut ini. 141 Menulis persamaan linear serentak dalam bentuk matriks.
6 xy 0. Bil Persamaan Linear Ya Tidak 1 𝑎 2𝑏 8 4𝑎 6𝑏 12 2 4𝑢 3𝑣 9 6𝑢 𝑤 5 3 2𝑑𝑒 8𝑑 3 𝑑 𝑒 12 4 𝑥 6𝑦 𝑥 12 42 242 Selesaikan persamaan linear serentak dengan menggunakan kaedah berikut. Persamaan linear serentak yang dibentuk.
Pada pembahasan kali ini kita akan menggunakannya untuk menyelesaikan sistem persamaan linear dua variabel dan tiga variabel. Salah satu caranya adalah dengan menggunakan kaedah mat. Menghitung nilai pembolehubah Other contents.
Jadi solusi dari dua persamaan linear dua variabel 2x. Matriks ialah satu set nombor yang disenaraikan dalam bentuk segiempat. Dua persamaan linear serentak boleh ditulis dalam bentuk persamaan matriks.
Jadi x 4 y 2. Persamaan matriksnya adalah Perhatikan bahwa dengan menghitung perkalian matriks di ruas kiri akan menghasilkan sistem persamaan linear seperti yang di awal. Tidak mempunyai solusi jika nilai determinan matriks sama dengan nol.
5x 1y 8z 46 4x 2y 12 6x 7y 4z 50. Contohnya untuk sebuah matriks yang mempunyai sebagian baris dan n yaitu sebagai kolom maka dapat dituliskan m x n atau dapat disebut dengan matriks atau dengan ordo m x n. Untuk sistem persamaan linear berikut.
Ax by. 6 xy 0 xy 6 y 6 x Mencari. 2y 3x 12.
28 Penyelesaian Persamaan Linear Serentak dengan Kaedah Matriks. Menyelesaikan bentuk persamaan linear 2 pembolehubah. Tentukan nilai x dan y dari persaan berikut ini.
Video ini menerangkan cara mudah untuk memahami cara melakukan soalan yg melibatkan persamaan serentak linear menggunakan kaedah matriks. B Tulis persamaan linear serentak berikut dalam bentuk matriks. Dalam notasi matriks ini dapat ditulis sebagai AX B.
Biasanya pada persoalan matematika ini menggunakan dengan matriks ialah untuk mencari nilai pada persamaan linear fungsi linear maupun transformasi linear. Karena melibatkan matriks dan determinannya maka pembaca dianggap sudah memahami konsep matriks. Sebagai contoh dalam persamaan linear serentak.
Penyelesaian masalah persamaan linear serentak dapat diselesaikan dengan menggunakan pelbagai kaedah. Mempunyai tak hingga solusi jika. Perkalian matriks dengan matriks.
56 p 50 q 502 60 p 48 q 510 Persamaan matriks yang sepadan ialah 5660 5048 qp502 510 Selesaikan persamaan matriks. Matriks Menyelesaikan persamaan linear serentak menggunakan kaedah matriks ID. PENYELESAIAN MATRIKS PERSAMAAN LINEAR 2 DAN 3 VARIABEL.
Sistem Persamaan Linear Dua Variabel. Ambil dua persamaan dalam matriks tipsnya adalah pilih persamaan yang akan memudahkan perhitungan. Beberapa buku teks merujuk kepada kaedah penyingkiran sebagai kaedah penambahan kerana ia melibatkan penambahan persamaan atau pemalar pelbagai persamaan ke atas satu sama seperti yang diperincikan lagi di dalam artikel ini.
Katakan A menunjukkan matriks. Langkah ke 2. Menyelesaikan Persamaan Linear dengan Microsoft Excel.
Mempelajari serta mengetahui cara-cara menyelesaikan persamaan linear menggunakan kaedah-kaedah tertentu. 3x 2y 5 9x y 1 Seterusnya menggunakan kaedah matriks hitung nilai x dan nilai y. Penyelesaian persamaan linear dua variabel dengan cara invers matriks.
Misalnya kita memiliki sistem persamaan linear berikut ini. Di penghujung unit ini pelajar seharusnya boleh. Q 142 Menentukan matriks p h p a b dalam k q c d dengan menggunakan matriks songsang.
Bentuk matriks dari persamaan SPLDV pada soal adalah sebagai berikut. B1001 - BASIC ALGEBRASIMULTANEOUS LINEAR EQUATION 1 Persamaan Serentak Linear Objektif Am. Untuk lebih jelasnya mengenai menyelesaikan persamaan linear dua variabel dengan menggunakan invers matriks atau metode invers perhatikan contoh soal yang telah disertai pembahasan berikut Contoh 1 Dengan menggunakan metode invers tentukan penyelesaian dari sistem persamaan linear dua variabel 2x - 3y 3 x 2y 5 Pembahasan.
Mengubah persamaan linear kebentuk matriks. Menentukan invers dari matriks yaitu. A m 6 2 3.
Matriks dapat digunakan untuk mempermudah dalam menentukan penyelesaian sistem persamaan linear. Umumnya penyelesai meggunakan samada kaedah grafik kaedah matriks kaedah penggantian atau kaedah penyingkiran. Mempunyai satu solusi jika nilai determinan matriks tidak sama dengan nol.
A Cari nilai m dan nilai n. Diberi bahawa matriks P 6 3 5 2 dan matriks Q 1 m 2 3 5 n dengan keadaan P Q 1 0 0 1. Cari harga sebatang pen dan sebatang pencil menggunakan kaedah matriks.
Secara umum solusi dari sistem persamaan linear dengan dua variabel adalah sebagai berikut. Selanjutnya akan diselesaikan SPLDV di atas menggunakan matriks. Langkah ke-3 mengalikan kedua ruas pada persamaan dengan invers matriks.

Matriks Kelas 11 Matriks Koefisien Sistem Persamaan Linear Youtube
Komentar